Simultaneous manipulation of multiple degrees of freedom of light lies at the heart of photonics. Nonlinear wavefront shaping offers an exceptional way to achieve this goal by converting incident light into beams of new frequencies with spatially varied phase, amplitude, and angular momenta. Nevertheless, the reconfigurable control over structured light fields for advanced multimode nonlinear photonics remains a grand challenge.
In our article titled "Nonlinear geometric phase coded ferroelectric nematic fluids for nonlinear soft-matter photonics," we propose the concept of nonlinear geometric phase in an emerging ferroelectric nematic fluid, of which the second-order nonlinear susceptibility carries spin-dependent nonlinearity phase (Fig. 1).
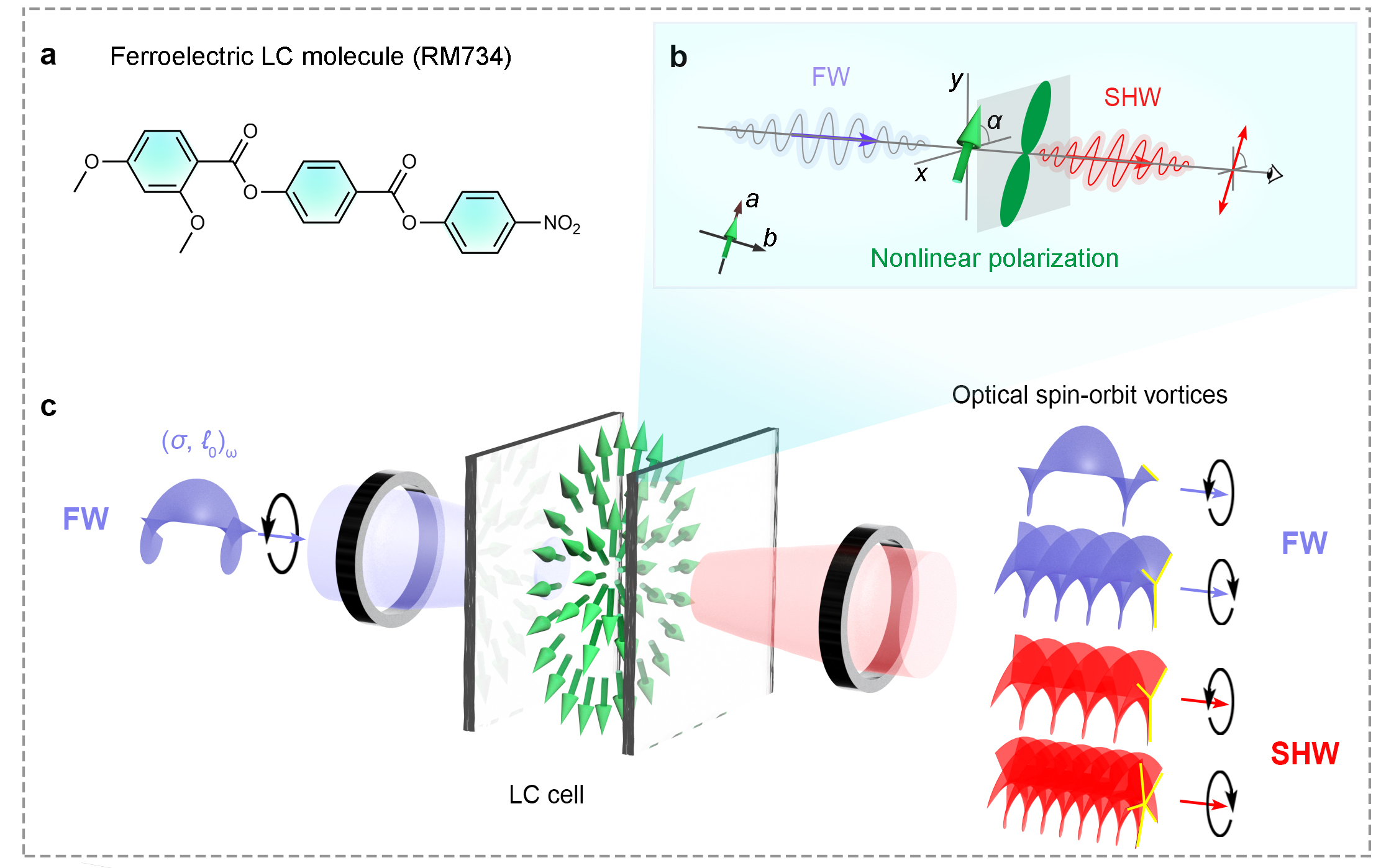
Fig.1|Ferroelectric nematic liquidcrystal for nonlinear soft-matter photonics. a, Chemical structure of the FNLC RM734 material. b, SHWs from the polar RM734 material under the pumping of the linearly polarized FW. The nonlinear polarization is along the polar direction of LC. c, Generation of SHWs with multiple spin-orbit angular momentum states with a nonlinear LC q-plate. For the incident FW with an angular momentum state of (σ, ℓ0)ω, the SHWs have specific angular momentum states due to the spin-orbit interactions of both FW and SHWs. σ = ±1 stands for the circular polarization state of light.
A case study with photopatterned q-plates demonstrates the generation of second-harmonic optical vortices with spin-locked topological charges using cascaded linear and nonlinear optical spin-orbit interactions (Figs. 2a and 2b). As shown in Figs. 2c and 2d, for the FW with angular momentum state of (+1, 0)ω, the measured states of modulated FW and generated SHW include (+1, 0)ω, (−1, +2)ω, (+1, +1)2ω, and (−1, +3)2ω. The measured SH conversion efficiency of the FNLC superstructure is up to ~ 10−4, and we expect that it can be further improved by introducing the phase-matching condition. We also investigate the high-order nonlinear spin-orbit interaction using the FWs with angular momentum states of (+1, +1)ω and (−1, +1)ω (Figs. 2e and 2f).
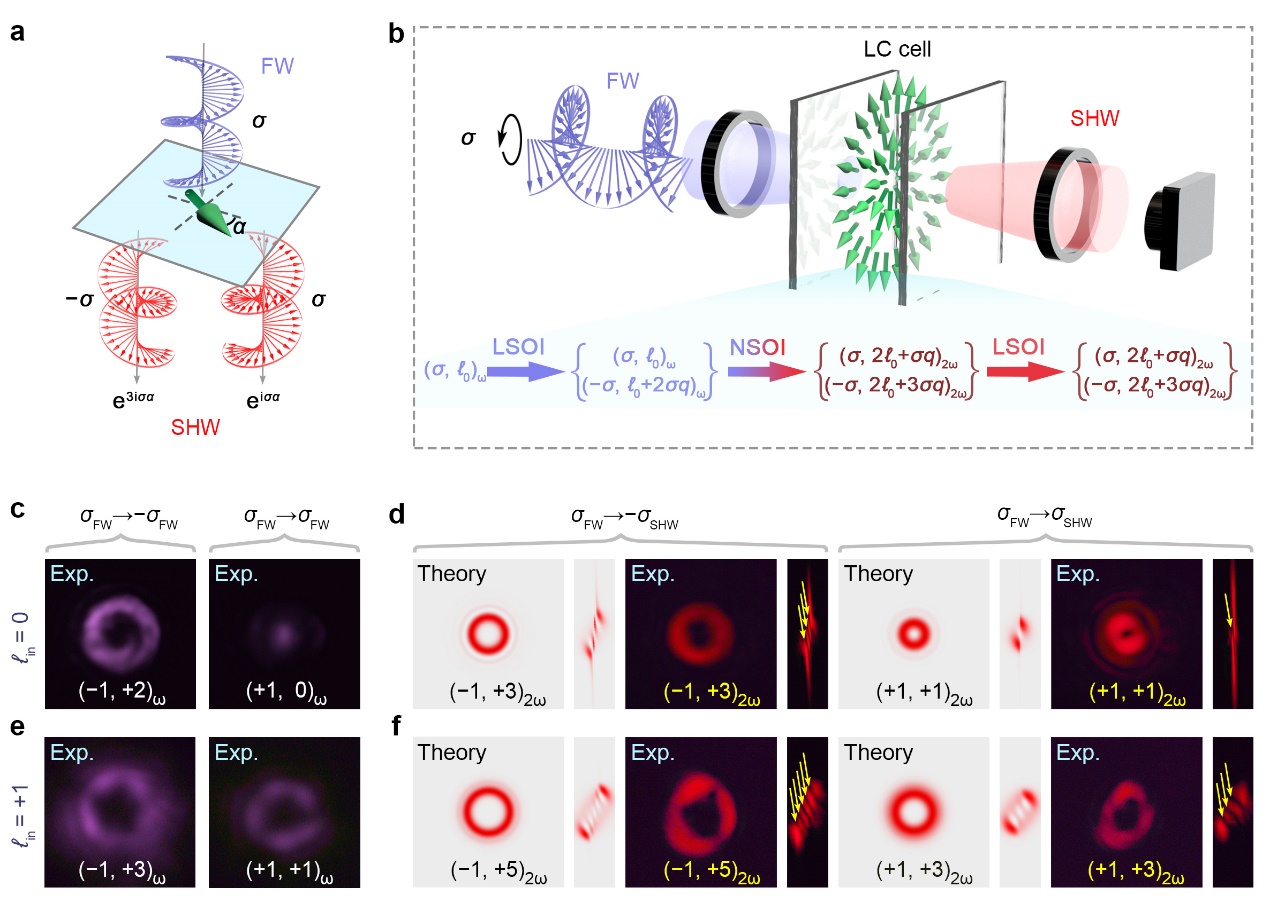
Fig.2|Geometric phase coded nonlinear optical spin-orbit interaction and the generation of SHoptical vortices with the FNLC q-plate. a, Generation of the SHWs with spin-locked nonlinear geometric phase. b, Illustration of the spin-orbit coupling and the light-matter interaction geometry between the circularly polarized FW and the nonlinear LC q-plate. LSOI: linear spin-orbit interaction. NSOI: nonlinear spin-orbit interaction. c,d, Linear and nonlinear geometric phase associated optical vortex generation in the FNLC q-plate. The angular momentum state of the incident FW is (+1, 0)ω. The abbreviation “Exp.” represents the experimental results. e,f, Linear and nonlinear geometric phase associated optical vortex generation in the LC q-plate. The angular momentum state of the incident FW is (+1, +1)ω.
Furthermore, we report particularly the dynamic tunability of second-harmonic structured light through temperature, electric field, and twisted elastic force (Figs. 3 and 4). The proposed strategy opens new avenues for reconfigurable nonlinear photonics, with potential applications in optical communications, quantum computing, high-resolution imaging, etc.
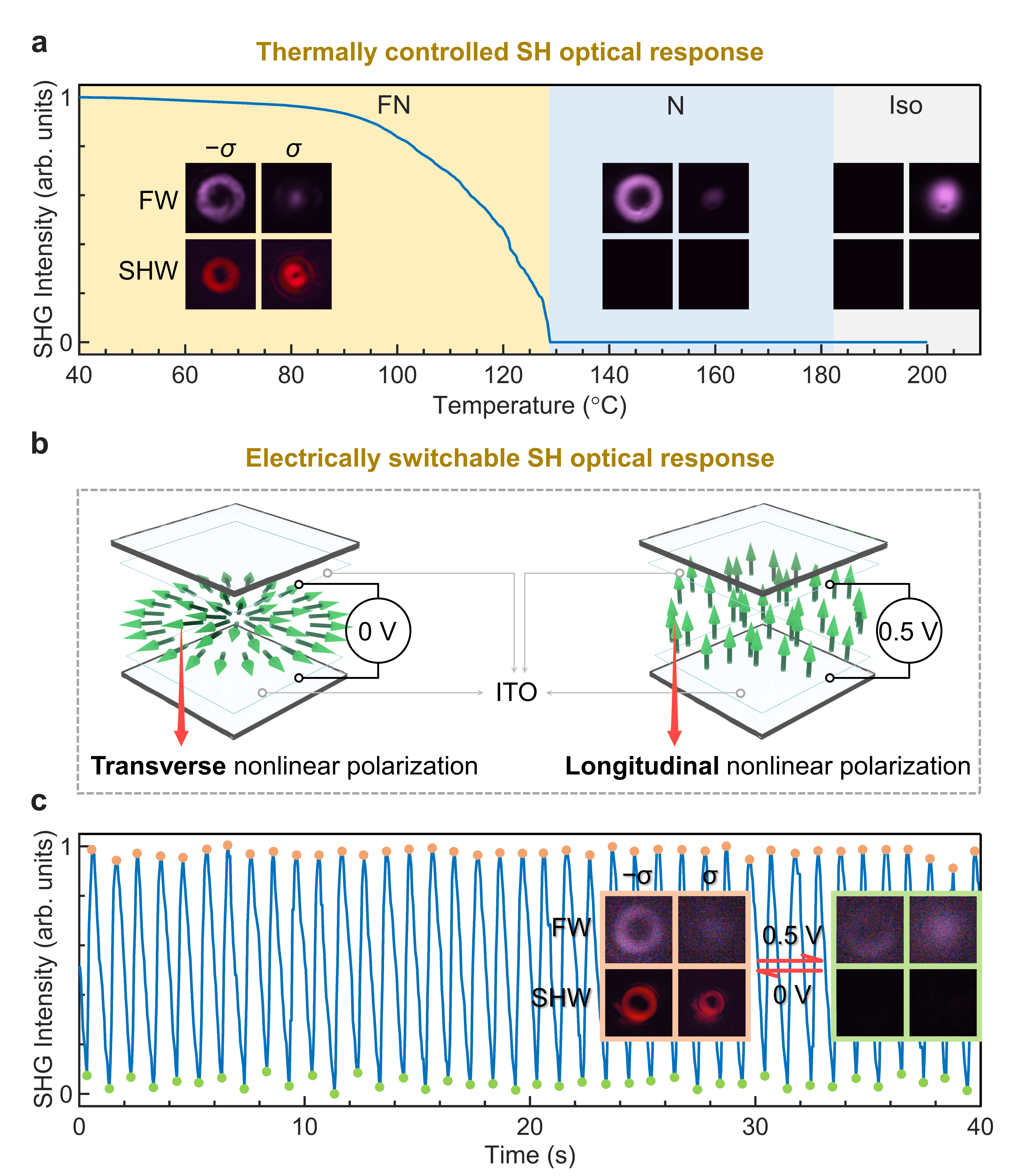
Fig.3|DynamicallyswitchableSHopticalresponseofthenonlinearLCq-plate.a, Thermally switchable FW and SH vortices. FN: ferroelectric nematic phase. N: nematic phase. Iso: isotropic phase.b, Schematic illustration of the electrically switchable nonlinear LC q-plate. c, Periodic switching of the intensity of the SH vortices by electrically tuning the spontaneous polarization of ferroelectric nematic q-plate from the transverse direction to the longitudinal direction. Source data are provided as a Source Data file.
Fig.4|Elastic force-drivenspin-selectiveSHopticalresponseofthe chiralLCq-superstructure.a, Schematic illustration of the three-dimensional chiral LC q-superstructure and the spin-selective generation of the SH optical vortex beams. b,c,left Calculated andmeasured intensity distributions of spin-selective SH vortices under the pumping of FWs with -handed circular polarization (LCP) and right-handed circular polarization (RCP) states. The abbreviation “Exp.” represents the experimental results.
Over the years, our group, led by Professor Yan-Qing Lu, has focused on optical micro- and nanostructures, such as liquid crystals, dielectric superlattices, and metasurfaces, to explore the underlying physical mechanisms of light-matter interactions. Recently, our group demonstrated the geometric phase associated nonlinear optical responses in the ferroelectric nematic LC q-plate, which allows for a series of cascade spin-orbit interactions enabling the simultaneous manipulation of various degrees of freedom of light, including amplitude, phase, polarization, orbital angular momentum, and frequency conversion. The unique structured vector vortex beams and spin-orbit-locked optical vortices with different topological charges are systematically investigated in the SHG process. By taking advantage of the high-precision and arbitrary photopatterning technique, we can achieve more functional nonlinear geometric phase-encoded LC architectures for desired nonlinear optical applications. Remarkably, we explore the thermal, electrical, and elastic force switching of the spin-orbit optical vortices with the planar q-plates and chiral q-superstructure, demonstrating the capability of dynamic wavefront engineering. The proposed soft-matter platform and the concept of nonlinear geometric phase in the FNLCs not only broaden the fundamental understanding of dynamic light-matter interactions in the framework of nonlinear optics but also open new avenues for developing reconfigurable nonlinear photonic devices. More applications, ranging from nonlinear vortex source, super-resolution imaging, to quantum information processing, are expected to be developed based on the proposed nonlinear soft-matter platform.
This work titled “Nonlinear geometric phase coded ferroelectric nematic fluids for nonlinear soft-matter photonics” was published in the latest volume of Nature Communications journal (https://doi.org/10.1038/s41467-024-53040-8).
J.-T. Pan, B.-H. Zhu, L.-L. Ma. et al. Nonlinear geometric phase coded ferroelectric nematic fluids for nonlinear soft-matter photonics[J]. Nature Communications 15, 8732 (2024).

