拓扑不变量是拓扑物理学的重要基本概念,源自于体能带波函数在布里渊区绝热演化所积累的几何相位。近日,菠菜担保网论坛的合作团队,提出了一种基于声学时变耦合相位构造合成布里渊区的普适办法,通过波函数的绝热演化精确测量了Zak phase、 Chern number等阿贝尔拓扑不变量,推广并验证了一种表征非阿贝尔拓扑荷的规范无依赖新方法。
不同于动力学相位,拓扑系统中的几何相位(亦称贝里相位,Berry phase)是指量子态绝热演化所累积的额外相位,即贝里曲率的积分。它表现了波函数在布里渊区的整体拓扑性质,而非局部细节。这一相位在凝聚态物理以及声波、光波等经典波的类量子模拟中发挥了重要作用。例如在具有手征对称性的一维系统中(如经典的SSH模型),波函数的几何相位也叫做Zak相位,在平庸和非平庸相分别量子化为0或π。在二维系统中,贝里曲率的面积分被称为陈数,也可由一个方向的贝里相位随另一个方向的演化所揭示,即所谓Wilson loop法。根据体边对应关系,实空间系统界面两侧拓扑不变量的差值决定了边界态的存在与否。
近几年的研究将这些概念扩展到非阿贝尔(Non-Abelian, NA)情况。此时多个能带的拓扑性质可由单一拓扑荷来描述,并且实空间边界态的个数由相邻系统的拓扑不变量的商决定,满足非阿贝尔交换关系。到目前为止,非阿贝尔拓扑不变量的表征主要依赖于观察本征波函数的绝热演化,如何开发新型规范无依赖的表征手段仍然有待探索。尽管几何相位在拓扑物理学方面举足轻重,但如何通过绝热演化对其进行直接测量仍然充满挑战。
为了观测拓扑波函数的绝热演化,我们首先提出了一种构造合成布里渊区的普适方法。以一个一维紧束缚模型为例,如图1所示,其元胞包含N个原子,从哈密顿量中可以看出布里渊区k即等价于元胞最外侧1和N之间复共轭的耦合相位。通过电声反馈电路设计耦合,这个元胞模型可以在声学腔系统中直接构造出来。特别地,当k连续地变化2π范围,等效于“遍历”了一次布里渊区。通过激发并观测波函数的绝热演化,我们便可以直接地测量能带的几何相位,即拓扑不变量。在实验系统中,该耦合相位k的连续变化由新开发的瞬态相位调制器(Transient Phase Modulator, TPM)来完成。

图1 由时变耦合相位构造合成布里渊区。上图是一个一维紧束缚模型,其中虚线框标示出包含N个原子的元胞。下图展示了该元胞的声学实现,其中红色反馈电路用于为腔体引入增益,蓝色(绿色)电路分别用于实现元胞内(元胞间)耦合。在连接最外两个腔体的耦合电路中插入了一个双通道TPM,用于引入瞬态相位调制k±(t) = ±4πt(测量结果见插图),从而“遍历”布里渊区。
我们首先考虑了一维SSH模型中Zak相位的测量。SSH模型的元胞包含两个声腔,通过调节胞内(v)和胞间(w)耦合强度的差值(2∆),可以实现拓扑相变。在实验中,我们首先激发k= 0参数下初始本征态(+和-分别标记上、下能带),然后关闭声源并记录两腔信号随耦合相位k± = ±4πt的演化(图2b)。通过在波函数总相位中剥离动力学部分,便可以提取体能带的Zak相位β±。对于∆ = -3Hz,系统处于拓扑平庸相,测得Zak相位为β± ≈ 0 (图2c);而当∆ = 3Hz时,系统进入拓扑非平庸相,对应的Zak相位为β± ≈ π(图2d)。这些实验结果与理论预测一致,证实了利用绝热演化测量拓扑Zak相位的可行性。需要指出的是,此过程的关键是演化需满足绝热条件,也可以通过带间跃迁参数μ定量分析(详情见文章附件)。

图2 SSH模型Zak相位测量。(a)SSH模型的能带图,参数为∆ = ±3Hz。(b)下能带波函数的激发(k± = 0当t<0)和演化(k± = ±4πt当0<t<0.5s)。(c-d)波函数含时演化期间,两腔之间的相位差。测量值(标记点)与理论值(曲线)一致,证明了绝热性。相应能带的Zak相位如图中标注。
我们进一步研究二维拓扑系统陈数的测量。以三能带耦合调制型AAH模型为例,其耦合设为vj(φ) = v0 +vmcos(2πj/3+φ)。其中φ与布里渊区k一起构成二维参数空间。将φ离散化,测量波函数沿k演化的Berry相位β,β(φ)的缠绕方式即反应了能带的陈数。实验中,我们使用三个声学腔构造其元胞,耦合连接方式如图3(a)。设v0 = vm=5Hz,该哈密顿量的能带结构如图3(b)所示,其从下到上体能带的陈数分别为1、-2和1。同样设置k± = ±4πt,计算得能带间跃迁系数均满足μ<<1,表明布络赫态演化满足较好的绝热性,如图3(c)。我们将φ离散为20个点,并提取了三个能带的贝里相位βn(φ)。结果显示,能带I和III的β(φ)在[-π, π]范围内完整绕行一圈(图3d和f),符合陈数为1的理论预测;能带II则反向绕行了两圈,与陈数-2一致(图3e)。此外,当φ=π时,所有能带的贝里相位均为 0,对应元胞间耦合为零的状态。总之,实验结果与理论完全吻合,证明该方法提取贝里相位的通用性,亦可推广到其他二维拓扑模型,如Haldane模型和Kane-Mele模型。
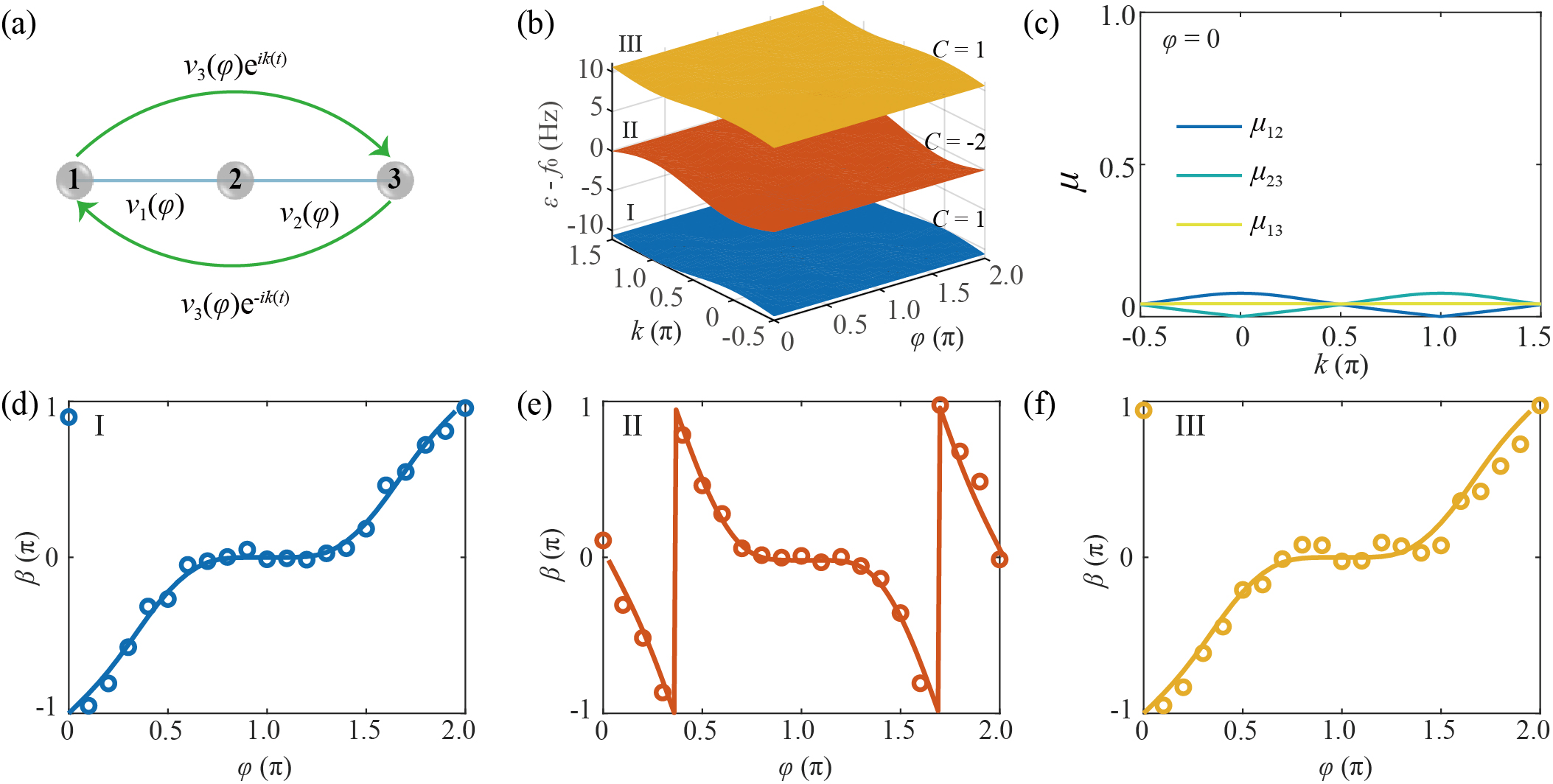
图3 二维系统陈数测量。(a)耦合调制AAH模型元胞的紧束缚示意图。(b)以动量k和相位ϕ为参数,元胞的能带图,其中标注了相应能带的Chern数。(c)在ϕ=0条件下两两能带之间的非绝热跃迁。相位调制为k±(t) = −0.5π±4πt。(d-f)实验提取(空心圆)和理论计算(实线)的三条能带的Berry相位随参数ϕ的变化,反映了第二条能带(e)的陈数为-2,其他两条能带(d和f)的陈数为+1。
最后,我们将拓扑不变量的测量推广到了非阿贝尔范畴。对于满足PT对称性的多带拓扑系统,各能带整体的拓扑性质可由NA拓扑荷来表征。这些拓扑荷可以通过观察本征态在球面上旋转来确定。在本文中,我们提出了一种规范无关的新方法,即通过SO(3)流形上的绝热演化路径来判断拓扑荷(具体理论推导见原文附件)。作为验证,我们构建了一个满足PT对称的三能带紧束缚模型,如图4(a)所示,其中v是元胞内耦合,w1和w2分别是元胞间最近邻和次近邻耦合强度。Δf是中间二号腔的频率失谐量。我们保持v小于w1或w2,该模型可简化为在一个非平庸SSH模型中插入一个失谐量为Δf的第三腔。在忽略w2且其他参数固定的情况下,仅通过改变Δf,即可得到i、j和k三种不同的NA拓扑相,如图4(b)所示。通过激发系统的本征态并驱动其沿着k绝热演化,我们直观地证明了其拓扑性质。如图4(c)所示,i相表现为第一个本征态在本征球面上构成一个完整的循环,而其他两能带的末态则仅演化到初态的对跖点;亦可以表现为SO(3)球中从球心沿着i方向演化到球面。对于j和k相,结论类似,如图4(d-e)。对于构造-1相,则仅需要忽略w1并设w2>v,其实验结果如图4(f)所示。

图4 非阿贝尔拓扑荷测量。(a)非阿贝尔三能带系统的紧束缚模型。(b)系统随∆f变化的NA相图。实线和虚线分别表示两个能隙的最小宽度。其他参数见正文。(c)左侧为非阿贝尔i相的系统能带。中间展示了在球面上的本征态轨迹,其中第一个本征态(蓝色)在绝热遍历布里渊区(BZ)时完成一个完整的循环,第二和第三本征态(棕色和黄色)旋转到初始状态的对跖点。拓扑荷还可以表现为SO(3)球中的绝热轨迹R(k),颜色从蓝到红标示k从0到2π的变化(右侧)。(d-f)类似于(c),分别是NA拓扑相j (d)、k (e)和-1 (f)的能带和实验结果。
综上所述,我们基于声学腔时变耦合相位构造了合成布里渊区,并通过绝热演化的方法直接测量了布络赫波函数的拓扑不变量,如Zak相位和陈数。我们还提出了一种规范无依赖的识别非阿贝尔系统拓扑荷的方法,并构造了一个三能带模型进行了实验验证。该理论是传统实规范方法的重要补充,为非阿贝尔拓扑系统的研究提供了新的依据,并有望适用于其他非阿贝尔编织过程。该工作得到了科技部重点研发计划、国家自然科学基金、中国博士后面上基金以及江苏省卓越博士后项目等资助。
相关工作以“Direct measurement of topological invariants through temporal adiabatic evolution of bulk states in the synthetic Brillouin zone”为题,发表在Physical Review Letters上。菠菜担保网论坛陈召宪副研究员、孙晓晨副研究员、湖南大学张远洪博士和香港科技大学张若洋研究助理教授为论文共同第一作者,华中科技大学祝雪丰教授、湖南大学杨鑫教授以及菠菜担保网论坛陆延青教授为论文共同通讯作者。菠菜担保网论坛唐江山副研究员亦有重要贡献。
文章信息:https://doi.org/10.1103/PhysRevLett.134.136601


